Well, It appears January is the month of the Red/Black tree, because here I am with yet more Red/Black tree content! Since their introduction in 1978[1] the study of red/black trees generally focused on their isomorphism with 2-3-4 trees. And, while it was recognized that 2-3 tree’s could be made to fit the red/black framework the inability to implement them top-down left them effectively sidelined, until Sedgewick introduced Left Leaning Red/Black tree’s in 2008[2].
A History of 2-3 Trees as Red/Black Trees
In the beginning there was 2-3 trees. They were serendipitously discovered by Hopcroft in 1970[5] – around the same time as the B Tree family of search trees with which they share many properties. 2-3 Tree’s have many desirable properties that make them great data structures for in-memory searching. Unfortunately they are also rather difficult to implement directly in most modern programming languages. This is where Red/Black Trees entered the equation. Red/Black Tree’s take the concept of representing m-ary tree’s as binary trees, and extend it to search trees, making it possible to implement balanced m-ary search tree’s as binary search trees. Guibas and Sedgewick mention 2-3 trees in the 1978 paper originally introducing Red/Black trees but found them (at the time) to be inferior to 2-3-4 trees.
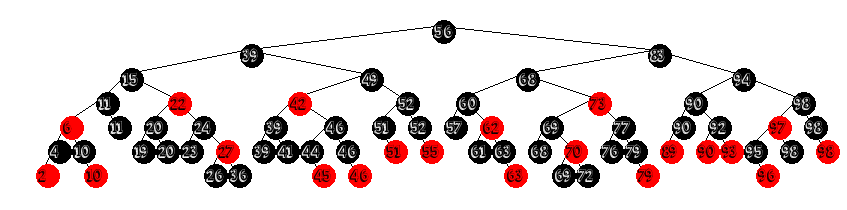
And there they stayed until Arne Anderson published his paper on AA trees, in which he detailed a set of algorithms which implemented the Red/Black rules with one addition: Red nodes can only be right children(sound familiar?). Anderson also removed the idea of “color” from the nodes, using instead a nodes “level” in the tree. While inspired by them. it can be argued that AA tree’s aren’t true Red/Black Trees.
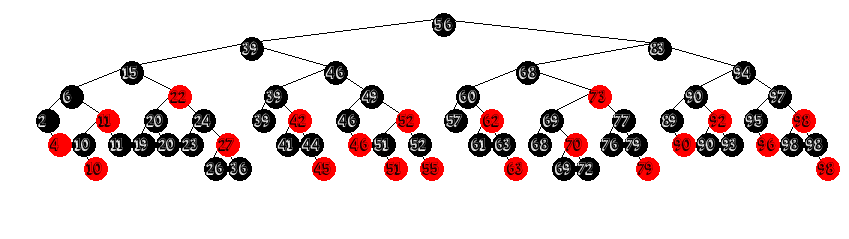
In 2008 Sedgewick introduced Left Leaning Red/Black tree’s, which took Arne Andersons Idea of enforcing the direction of red children (conveniently choosing the opposite of Anderson’s), and re-implementing it directly in the red black framework. This made for a much easier implementation than the original Red/Black algorithms thanks to eliminating symmetric balancing cases, reducing the number of conditions requiring rotations in half.
While the algorithms were simple to explain, It wasn’t long before people started noticing that something wasn’t quite right with their performance, particularly with respect to deletion.[3] As it turns out, the very thing that made for such a simple insertion algorithm was the self-same property that was strangling the performance of Left Leaning Red/Black trees: asymmetry. This shouldn’t have really come as much of a surprise, as AA tree’s had long been known to perform much worse than Red/Black trees. And Left Leaning Red/Black trees have similar performance to AA trees.
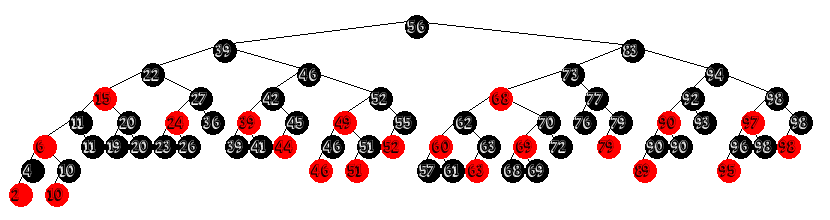
Sedgewick was eager to point out that Left Leaning Red/Black trees have a one-to-one correspondence with 2-3 trees. What he failed to mention in his 2008 papers is that you can do the same trick with right leaning Red/Black trees, and that in fact red nodes can lean in either direction in the same tree: the only condition separating 2-3 Red/Black tree’s from 2-3-4 Red/Black Trees is that a red node can have a red sibling in 2-3-4 trees, In 2-3 trees you cannot. It is this last point that bring us to the point of todays post: 2-3 Red/Black trees that may have red child nodes as both right and left within the same tree.
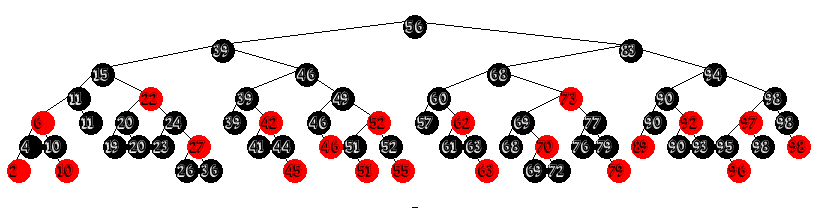
I found out about this class of Red/Black tree very recently, I can’t remember what it was I was searching for when I came across the article[4], but the author termed them “Parity Seeking 2-3 Red/Black Trees”. While the algorithms for maintaining balancing in them do have to handle more cases than is addressed by Left Leaning 2-3 trees, the logic behind the rotations is very simple, and don’t suffer the same performance hits that LLRB and AA trees have – performing on par with 2-3-4 red/black trees. I’ve blabbed on a bit longer than I meant to, so let’s stop talking about them and start implementing them!
Insertion in 2-3 Red/Black Trees
Insertion in these trees takes place bottom up – we perform a normal BST insertion, inserting a new node as a leaf which we color red. Once the that is done, we then proceed back up the path towards the root, fixing any violations of the Red/Black rules.
node* insert23(node* x, K key, V value) {
if (x == nullptr)
return new node(key, value);
if (key < x->key) x->left = insert23(x->left, key, value);
else x->right = insert23(x->right, key, value);
return fixInsert23(x);
}
node* insert(K key, V value) {
root = insert23(root, key, value);
root->color = black;
count++;
}
The papers authors use the iterative Red/Black Tree implementation from CLRS which balances purely bottom up as the foundation from which they created their 2-3 balancing rules. I have instead chose to implement the algorithms they described using a recursive approach without parent pointers, using my bottom up 2-3-4 Red/Black Tree implementation covered in a previous post as a starting point.
The bottom up balancing belies a beautiful simplicity in it’s logic of when to rotate. The algorithm for insertion follows a rather intuitive set of rules laid out by the authors of the original paper[4].
node* fixUp(node* x) {
x = makeRedChildrenLean(x);
x = makeRedParentSibling(x);
x = pushRedUp(x);
return x;
}
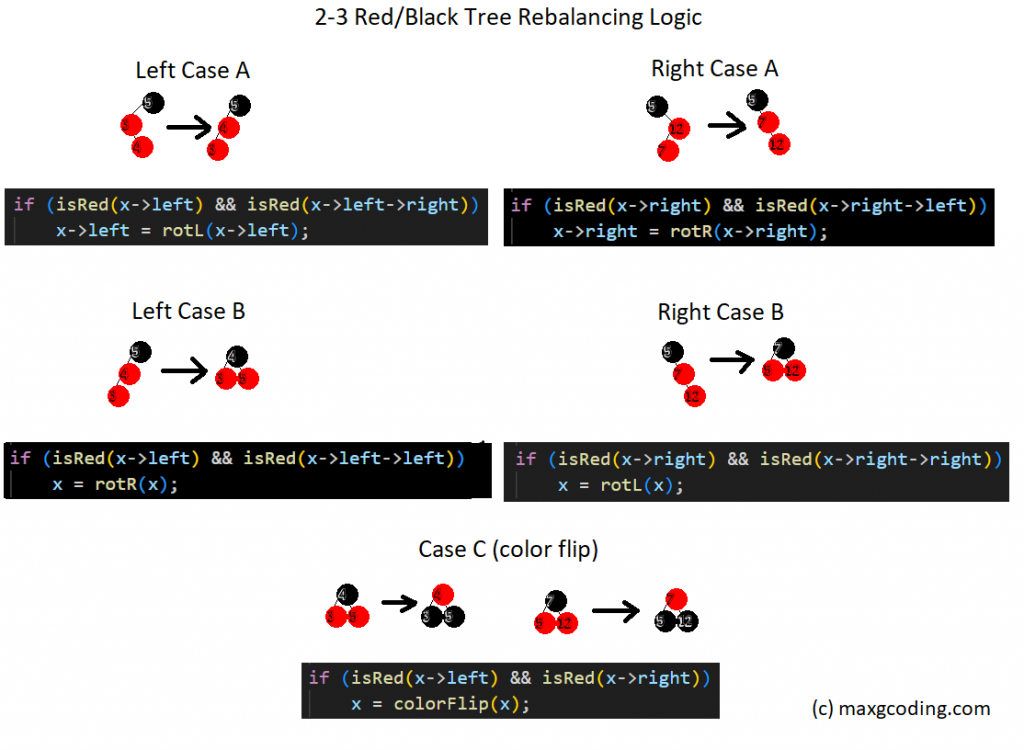
Regardless of which style you prefer – iterative or recursive – we have three conditions that will require rotations or recoloring. Case A and Case B have Right and Left mirrored cases while Case C is the same. The conditions described in the original paper are as follows:
Case A) If two nodes in a row are red, but are “bent”, we rotate the child node to make the two red nodes be “straight”.
node* makeRedChildrenLean(node* x) {
if (isRed(x->left) && isRed(x->left->right))
x->left = rotL(x->left);
if (isRed(x->right) && isRed(x->right->left))
x->right = rotR(x->right);
return x;
}
Case B) If two nodes in a row are red and leaning in the same direction, we rotate the parent node, turning the parent-child pair into siblings.
node* makeRedParentSibling(node* x) {
if (this->isRed(x->left) && this->isRed(x->left->left))
x = this->rotR(x);
if (this->isRed(x->right) && this->isRed(x->right->right))
x = this->rotL(x);
return x;
}
C) If a node has a red sibling, we do a color flip on the node, its parent, and its sibling, effectively pushing the red node “up” towards the root.
node* pushRedUp(node* x) {
if (this->isRed(x->left) && this->isRed(x->right))
x = this->colorFlip(x);
return x;
}
“But Wait!” I hear you saying, “Doesn’t having the root node be red violate the rules for red black trees?” And that is absolutely correct. It is for this reason that we end every insertion by coloring the root node black. This seemingly random final step is a safe guard against the event that during the rebalancing the root has become red – as in the example above. We can safely change the root’s color because it will increase the black length of all paths in the tree equally. This is the equivalent of when a B-Tree splits at the root and grows upwards.
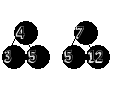
As you can see, once done we are left with a valid red black Tree. The helper methods used to perform rotations and color changes are exactly the same ones used for 2-3-4 Red/Black Trees and Left Leaning Red/Black Tree’s:
bool isRed(node* x) {
return (x == nullptr) ? false:(x->color == red);
}
node* colorFlip(node* x) {
x->color = !x->color;
x->left->color = !x->left->color;
x->right->color = !x->right->color;
return x;
}
node* rotR(node* x) {
node* y = x->left;
x->left = y->right;
y->right = x;
y->color = x->color;
x->color = red;
return y;
}
node* rotL(node* x) {
node* y = x->right;
x->right = y->left;
y->left = x;
y->color = x->color;
x->color = red;
return y;
}
If you’re still curious of what exactly each rotation accomplishes I’ve made this handy graphic to help explain how the rotations and color changes effect the structure of the tree, showing the tree before and after the changes are applied and the relevant line of code that precipitated it:
Bonus 2-3-4 Trees!
Just as Sedgewick noted that by changing the placement of the color flip changed his Left Leaning Red Black Tree from a 2-3-4 to a 2-3 tree, you can convert parity seeking 2-3 tree’s into 2-3-4 trees by checking and handling case C before cases A and B:
node* fixInsert23(node* x) {
if (isRed(x->left) && isRed(x->right)) //doing case c first yields a 2-3-4 tree!
x = colorFlip(x);
if (isRed(x->left) && isRed(x->left->right)) //case a
x->left = rotL(x->left);
if (isRed(x->right) && isRed(x->right->left))
x->right = rotR(x->right);
if (isRed(x->left) && isRed(x->left->left)) //case b
x = rotR(x);
if (isRed(x->right) && isRed(x->right->right))
x = rotL(x);
return x;
}
I’m unsure if the original authors missed this point, or if they did, they didn’t feel it worth mentioning in a predominantly 2-3 tree focused article. Oddly enough, the code snippet they included in the original article is actually the 2-3-4 variant, despite being labeled as the 2-3 fix up routine! It is because they also discussed 2-3-4 tree’s in their paper I believe it to be a labeling error on their part, one which I only discovered after doing side by side analysis of my own implementations of parity seeking 2-3 Red/Black, bottom up 2-3-4 Red/Black, and bottom up 2-3 LLRB trees.
In any case, that’s what I got for today. The article I found this variant in is linked below as number 4, and contains a full treatment on deletion as well and is definitely worth the read.
If you’re interested in my implementations of bottom up red/black tree’s they are available on my github.
Until next time, Happy Hacking!
Further Reading
[1] Guibas, L., Sedgewick, R. “A di-chromatic framework for balanced trees”, 1978, https://sedgewick.io/wp-content/themes/sedgewick/papers/1978Dichromatic.pdf
[2] Wayne, K., Sedgewick, R. “Algorithms” 4th, ed. 2008. Ch 3 “Searching”
[3] Kohler, Eddie. “Left Leaning Red-Black Trees Considered Harmful” – https://read.seas.harvard.edu/~kohler/notes/llrb.html
[4]Gandhi, et. Al “Revisiting 2-3 Red-Black Trees with a Pedagogically Sound yet Efficient Deletion Algorithm: The Parity-Seeking Delete Algorithm”, 2022, https://arxiv.org/pdf/2004.04344.pdf
[5] Aho, Hopcroft, Ullman “Data Structures And Algorithms”, 1982, Addison-Wesley, Ch. 5, section 4, pp. 169 – 180
