Comparing Balanced Search Tree Algorithms

mgcadmin 11-03-2023

There is a long standing debate amongst developers on which Self Balancing Binary Search Tree is better: AVL Trees or Red Black Trees. It's one of those age old debates the inspires religious like fervor in those which choose a side.

The situation only became more complicated with the introduction of Left Leaning RedBlack trees, a variant of RedBlack trees aimed at simplifying the implementation for the developer.

Conventional wisdom holds that for search heavy applications, the AVL tree will perform better than Red Black Tree's because it's balancing rules are stricter, resulting in a slightly bushier tree. Conversely, Red Black tree's will shine in applications that require lots of inserts and deletes as its looser balancing rules results in fewer rotations.

This of course is purely conjecture, extrapolated out from the hidden constants in the analysis of both algorithms. Self balancing binary search trees have a worst case tree height O(log N). AVL trees have an average height of 1.44 log N, with red black trees being closer to 2 log N.

And that is pretty much the breadth of the information you'll find when researching the subject. So I decided to take a closer look.

Popular Implementations

Sure, differences in height bounds explains some of the differing performance, but what other factors can cause differences? What about choice of implementation? Is the algorithm top down or bottom up? Recursive or iterative?

By far the most commonly encountered implementation of Red Black trees are those based on the algorithms introduced by Cormen et. al in CLRS. This algorithm is what every version of the C++ standard template library version of map and set containers, Java's TreeMap and TreeSet in the java collections library, and OpenBSD's sys/tree.h are based on. And its a monster. The level of complexity in this particular implementation are what inspired the development of Left Leaning Red Black trees.

This is far from the only RedBlack tree algorithm though. In fact, if you were to look at the four different editions of Sedgewick's book "Algorithms" you'll get three different implementations:

• The 1st & 2nd edition of his book implements an iterative one-pass top down algorithm that performs all balancing operations on the way down the tree.
• The 3rd edition version is a recursive bottom up implementation that splits 4 nodes on the way down the tree but performs all rotations as the stack unwinds back up the tree after insertion.
• The 4th edition presents a bottom up recursive implementation of left leaning red black trees that performs ALL tree manipulations on the way back up the tree.

When it comes to AVL trees libavl is by far the most popular "off the shelf" implementation. Being a C library it IS usable in any language that can hook into the C ABI, though it is still far from an ideal solution being a non-OOP approach. This isn't really a blocker to anyone desiring to use an AVL tree however, as their implementation is very straight forward.

Still, one cant help but wonder: why are there so few AVL trees in common use compared to RedBlack trees?

I have only seen AVL tree algorithms that perform balancing operations on the way back up the tree after performing a normal BST insertion. If anyone knows of an implementation that performs balancing on the way down the tree, please forward it to me, i would be interested in seeing how its done.

Implementations used in the study

The purpose of this study is to compare the algorithms themselves against each other. I wanted to compare the performance of recursive vs iterative implementations as well as the various tree types.

To this end, I prepared my own versions of Iterative AVL and Iterative LLRB trees. The recursive versions of those two algorithms are C++ translations of the Java code that appear in Algorithms 4th edition by Robert Sedgewick. (https://algs4.cs.princeton.edu/33balanced/)

The iterative Red Black tree is based on the example in 2nd edition of "Algorithms in C++" by Sedgewick. And lastly, std::map is the GCC STL implementation of Iterative Red Black Trees derived from CLRS by Cormen et. al.

Lets compare some of the structural properties of the different implementations used:

Tree Type	Parent Pointers	Sentinel Nodes	Balance Information	Balancing
Iterative AVL	Yes	No	Integer	Bottom up
Recursive AVL	No	No	Integer	Bottom up
Iterative LLRB	Yes	No	Boolean	Bottom up
Recursive LLRB	No	No	Boolean	Bottom up
Iterative RB	No	Yes	Boolean	Top Down
std::map	Yes	Yes	enumerated type	Bottom up

All of the code used in this study is available on my github at https://github.com/maxgoren/BalancedSearchTrees/

Time to insert N items

The first test i wanted to conduct was building a tree through insertions only to see what effect input size had on creating the tree. To achieve this I inserted random numbers in to each type of tree for different values of N, the results of which are displayed in the following image:

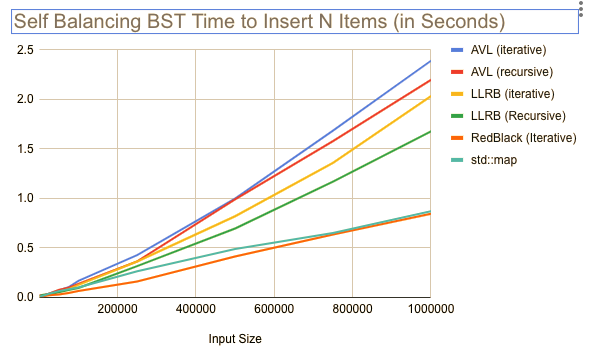
These are some pretty interesting results. When it comes to insert-only tree construction, Red Black trees were the clear winner. In the case of both LLRB and AVL trees, the recursive algorithm proved slightly faster than the iterative version.

Whats truly interesting is the growth of red black trees when compared to the other algorithms. The time taken to build the tree seems to be growing with a complexity of O(n) for the RedBlack trees, while the AVL and left leaning red black trees seem to be growing by O(n log n). An interesting aside, is that the two RedBlack tree implementations use sentinel nodes, while the AVL tree and Left Leaning Red Black tree implementations use null pointers to denote empty links.

It should be pointed out that for a given input set, there are more valid RedBlack trees than can be build when compared to Left Leaning Red Black trees due to the degree of freedom in the slanting of red nodes that is removed by the LLRB balancing rules. This means RedBlack trees may require fewer rotations to construct a RedBlack tree compared to Left Leaning RedBlack tree for the same set of keys, causing better insertion time performance for RedBlack trees than their left leaning brother.

Time to perform N searches

After seeing how each tree type performed when inserting elements, it was time to see how they handled searching for them, after all they ARE called a binary SEARCH tree!

This test was run similarly to the previous, except once the tree is built, we than perform N searches for random keys in the range of the ones we just inserted.

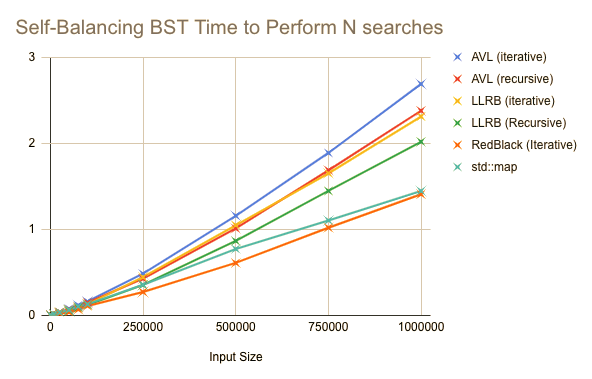
We are again treated to some interesting results. Recursive AVL trees and Iterative LLRB trees are neck in neck, but recursive LLRBs are almost 50% faster than than Iterative AVL trees.

As with the previous test iterative RedBlack trees come out on top. In fact, the two AVL trees are the two worst performing of the bunch, raising some doubt in the previously mentioned hypothesis that for search intensive applications that AVL trees should be faster, though more research needs to be done.

Wrapping Up

After running the tests and gathering final results, I can comfortable say that Original Red Black trees are the most performant of all types tested, with the parent pointer free implementation being the overall best performer.

It seems we can say fairly comfortable that the different constants in height bounds of AVL vs Red Black tree does NOT contribute to a better search times in AVL trees.

In the future I plan to test deletion performance, as well as general stress tests of each tree type, inducing worst case behavior in each tree type and compare the results. I would also like to add a test for deletion, but that requires more work in shaking out the bugs in my iterative deletion algorithms, as currently only my recursive implementations have bug-free re-balancing algorithms upon deletion, so that test must wait for the time being.

 

---