The 1978 paper “A Dichromatic Framework for Balanced Trees” by Guibas and Sedgewick[1] in which the authors introduced red/black trees to the world, they discuss algorithms for bottom up 2-3 tree’s, bottom up 2-3-4 tree’s, and bottom up AVL tree’s using the Red/Black framework as the mechanism for deciding when to rotate. In addition, the authors presented – and were primarily concerned with – top down algorithms for 2-3-4 red/black trees, as these were considered to posses more desirable properties.
Nearing the end of the paper the authors very briefly mention a variant of Red/Black tree’s which they call “Top Down Single Rotation Trees” and go on to claim that this variant requires 60% less code than what is needed for “traditional” AVL and 2-3 trees while offering comparable performance.
It was the authors desire to implement balanced red/black tree’s using only single rotations which led to this discovery. In order to eliminate double rotations, they allow two red nodes to occur in a row in the tree – so long as they slant in the same direction. It is only revealed that these “Top Down single rotation” trees are in fact 2-3-4-5 trees in the caption under a figure for “Program 7″[1].
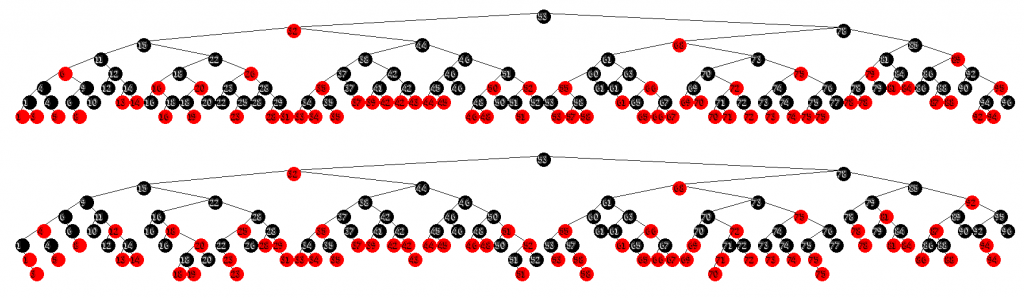
Bottom: 2-3-4-5 Red/Black Tree
Both Tree’s built from same input sequence using top-down insertion.
As far as I know, this is the only discussion of Red/Black 2-3-4-5 trees anywhere in published literature, and Sedgewick was nice enough to include an algorithm for top-down insertion – albeit in ALGOL (68?). Being the nice guy that I am, I’ve taken the liberty of implementing the insertion algorithm in C++ to share with all of you.
Top Down 2-5 Red/Black Insertion
With the exception of the node structure, these trees share no other code with the bottom up variants I’ve been discussing lately, with even the rotations being handled differently.
template <class K, class V>
struct rbnode {
K key;
V value;
bool color;
int N;
rbnode* left;
rbnode* right;
rbnode(K key_, V value_) {
key = key_; value = value_;
color = true;
left = nullptr; right = nullptr;
N = 0;
}
rbnode() {
color = true;
}
};
It is customary for iterative implementations of Red/Black Trees to use sentinel nodes as both a header and as sentinel nil nodes in the place of null pointers. While this would be more of an annoyance in a recursive implementation, for a Top/Down Iterative approach it makes our job much easier by allowing us to safely dereference certain links without having to perform additional checks, simplifying the code greatly. In addition to sentinel nodes, I’ve also made use of named accessor methods to make the code a little nicer to read and somewhat more in-line with the original ALGOL.
template <class K, class V>
class TopDown2345 {
private:
using node = rbnode<K,V>;
using link = node*;
link head, z;
link curr, parent, grand;
int count;
node* left(node* t) {
return t->left;
}
node* right(node* t) {
return t->right;
}
bool color(node* t) {
return t->color;
}
K key(node* t) {
return t->key;
}
bool isnil(node* x) {
return x == z;
}
node* rotate(K key, node* y);
void balance(K key);
public:
TopDown2345() {
z = new node(numeric_limits<K>::max(), numeric_limits<V>::max(), black, nullptr, nullptr);
z->left = z; z->right = z;
head = new node(numeric_limits<K>::min(), numeric_limits<V>::min(), black, z, z);
count = 0;
}
void insert(K key, V value);
};
If you’ve never used sentinel nodes in a binary search tree before, the reason we initialize head to the lowest possible value is because head is not the root node. Head points to the root node through its right link. Thus when we compare any value to head’s key, it will always result in a right branch. Z’s left and right pointers point back to it’s self, while head’s point to z. This allows us to de reference links like head->right->left->right->right without worrying about a possible null pointer.
During insertion we have to track some of our ancestors on our search path as they may be needed for recoloring/balancing. In 2-3-4 tree’s we needed to track the current node, its parent, grand-parent, and great-grand parent. Since 2-3-4-5 tree’s don’t perform double rotations, we no don’t need to track the current nodes great-grandparent anymore.
void insert(K k, V value) {
curr = head;
parent = curr;
grand = parent;
while (!isnil(curr)) {
grand = parent; parent = curr;
curr = (k < key(curr)) ? left(curr):right(curr);
if ((color(curr->left) && color(curr->right))
|| (color(curr) && color(curr->left))
|| (color(curr) && color(curr->right))) {
balance(k);
}
}
curr = new node(k, value, black, z, z);
if (k < key(parent)) parent->left = curr;
else parent->right = curr;
balance(k);
head->right->color = black;
count++;
}
If during insertion we encounter a node that has two red children or a red node with a red child, we call our balance routine which handles the re-coloring and rotations. Otherwise, insertion proceeds as normal for Iterative insertion, inserting the new node as a leaf. While 2-3 and 2-3-4 tree’s have newly inserted nodes colored red, 2-3-4-5 nodes are colored black upon insertion. Once installed at the leaf, we call the balance routine one final time before coloring the root node black and exiting.
It’s interesting that newly inserted nodes should be colored black, though inconsequential as upon calling balance after their insertion, we immediately change it’s color to red.
void balance(K v) {
if (color(curr) == black) {
curr->color = red;
curr->left->color = black;
curr->right->color = black;
} else {
curr->color = black;
parent->color = red;
}
if (color(curr) == black ||
(color(parent) == red && (v < key(grand) != v < key(parent)))) {
parent = rotate(v, grand);
}
head->right->color = black;
}
If on the other hand balance has been called during the search, and the current node is red, it will color it black and its parent red, setting it up for the next case, where if the current node is black, or we are the bottom node of two red’s which are slanting in the wrong direction, we perform a single rotation of the current nodes parent. The rotation method is interesting in that it “re-discovers” which direction it should rotate. This is the same rotation procedure in the earlier editions of Sedgewicks “Algorithms in C++”[2].
node* rotate(K v, node* y) {
node* gchild, *child = (v < key(y)) ? left(y):right(y);
if (v < key(child)) {
gchild = child->left; child->left = gchild->right; gchild->right = child;
} else {
gchild = child->right; child->right = gchild->left; gchild->left = child;
}
if (v < key(y)) y->left = gchild; else y->right = gchild;
return gchild;
}
Validating 2-3-4-5 Red/Black Trees
We can of course validate the resulting tree’s in the usual way by performing the following checks:
- Is the tree a valid Binary Search Tree?
- Does the tree have the same number of black nodes along every path from root to leaf? (Height Balanced)
- Are red nodes arranged according to the rules laid out in the paper?
The first two tests are exactly the same as for any other red/black tree. It is the newly allowed orientations of the red nodes that we must confirm is correct.
bool isBST(node* x) {
if (x == z)
return true;
if (x->left != z && x->key < x->left->key)
return false;
if (x->right != z && x->right->key < x->key)
return false;
return isBST(x->left) && isBST(x->right);
}
bool isBal(node* x, int bb) {
if (x == z)
return bb == 0;
if (!isRed(x))
bb--;
return isBal(x->left, bb) && isBal(x->right, bb);
}
bool blackBalance(node* root) {
int bb = 0;
node* x = root;
while (x != z) {
if (!isRed(x)) bb++;
x = x->left;
}
return isBal(root, bb);
}
Determining the red balance is also straight forward. If two red nodes occur in a row, they must “lean” the same direction. Other than that, we must ensure that no more than two red nodes line up.
bool isRed(node* x) { return (x == z) ? false:(x->color == true); }
bool is2345(node* x) {
if (x == z)
return true;
if ((isRed(x->left) && isRed(x->left->right)) ||
(isRed(x->right) && isRed(x->right->left))) {
return false;
}
if (isRed(x->left) && isRed(x->left->left) &&
(isRed(x->left->left->left) || isRed(x->left->left->right))) {
return false;
}
if (isRed(x->right) && isRed(x->right->right) &&
(isRed(x->right->right->right) || isRed(x->right->right->left))) {
return false;
}
return is2345(x->left) && is2345(x->right);
}
Wrapping Up
It’s a shame these tree’s have been practically forgotten to history as they are both a fun and interesting way of taking a different look at the red/black framework while showing the surprising degree of flexibility the framework posses. Being height balanced, they offer the same O(log N) worst case performance as the other balanced red black tree’s.
But here’s the rub: those pesky constants are it again. It’s known that for AVL tree’s the hidden constant is 1.44, and 2-3-4 Red Black Tree’s are O(2LogN). This is where the adage that AVL tree’s are better when search is the dominant use, and Red/Black tree’s are better for insertion heavy tasks comes from. Sedgewick speculates that for “Top Down single rotation tree’s” that hidden constant is 3. The practical real world implications of this are unknown, as for as far as I can tell, these trees never left the halls of academia.
Anyway, that’s what I’ve got for today. Until next time, Happy Hacking!
Further Reading
[1] Guibas, L., Sedgewick, R. “A di-chromatic framework for balanced trees”, 1978, https://sedgewick.io/wp-content/themes/sedgewick/papers/1978Dichromatic.pdf
[2] Sedgewick, R. “Algorithms” 2nd, ed. (1992) Ch. 15 “Balanced Trees”
