Binary search trees are a ubiquitous data structure in computer science. When it comes to maintaining ordered collections, it is the de-facto structure for implementation. Binary search tree’s have one fault however: if care is not taken to maintain balance, they have the potential to devolve into an even more in-efficient version of an ordered linked list. It is because of this tendency to become unbalanced that gave rise to the various tree balancing algorithms that are so prevalent today.
An unbalanced binary search tree can be brought back in to balance by applying a series of rotations to the unbalanced tree’s nodes. AVL Trees were the first “self balancing” binary search tree, and Red Black trees are arguably the most popular.
Half-Splay tree’s are another type of self balancing binary search tree, and the topic of todays post. Splay tree’s are a class of tree’s Introduced by Sleator & Tarjan in the mid 1980’s that take a radically different approach to self-balancing through the use of splaying. Half-splay tree’s are a related concept that uses single rotations instead of the double rotations of Splay tree’s – hence the name.
Fast Access Uber Alles
Splay Tree’s are designed with one thing in mind, and only one thing: Fast Access to recently accessed Items. Fast access equates to fast search times, and when it comes to binary search trees, fast access is a consequence of keeping the tree balanced. But is there any other way to speed up repeated access times besides balancing? Cacheing recently accessed items in the event that they will be needed again soon is one possibility, but how should we manage the cache? And that’s when the Sleator & Tarjan had a revolutionary idea: What if we implemented the “Move to front” heuristic from linked lists, in a binary search tree?
The move-to-front heuristic is used in linked lists to speed up repeated accesses of elements in a linked list by re-arranging the list each time it is accessed, to place the most recently accessed node at the beginning of the list. In a sequential access structure like a linked list, this can lead to significant savings.
iterator<T> get(T info) {
if (m_head->info == info) //Check if element we want is already first
return iterator<T>(m_head);
Node x = m_head;
while (x->next->info != info) x = x->next; //Find element we want
if (info == x->next->info) {
Node t = x->next;
x->next = x->next->next; //unlink the node
t->next = m_head;
m_head = t; //move it to the front of the list
return iterator<T>(m_head);
}
return end();
}
In an un-ordered linked list moving the most recently accessed element to the front of the list is straight forward, as seen in the above code snippet. But binary search tree’s maintain a strict ordering that we can’t violate: the search tree property (Left < root <= right must be maintained, otherwise we wont be able to binary search the tree.
So how can we move a node in a binary search tree while still maintaining the search tree property? As it turns out, we already know how to just such a thing: rotations!
Half-Splay trees via Root Insertion in Binary Search Trees
In my opinion, the term “root insertion” is a bit a misnomer, regardless that is what this technique was named – and it does have the effect of the value being added to the tree ending up as the root. What’s actually happening though is that a normal BST insertion is done, adding the new value as a leaf, and while this is where a normal BST insertion would end, we’re only half way done with root insertion.
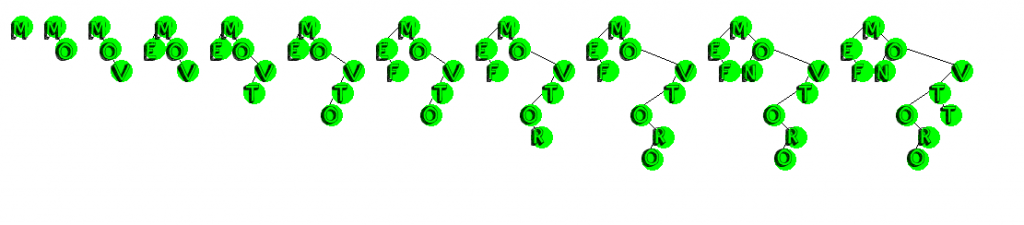

Once the node has been placed as a leaf, we then rotate the newly inserted node to switch places with its parent. This process of swap by rotation repeats until the value being inserted is at the root. Because rotations are guaranteed to preserve the binary search tree property, the end result is a valid binary search tree, with each insertion occupying the root position.
Node moveToRoot(Node h, T info) {
if (h == nullptr)
return h;
if (info < h->key) {
if (h->left) h = rotateRight(h);
} else {
if (h->right) h = rotateLeft(h);
}
return h;
}
Node put(Node h, T info) {
if (h == nullptr)
return make_node(info);
if (info < h->key) {
h->left = put(h->left, info);
} else {
h->right = put(h->right, info);
}
return moveToRoot(h, info);
}
We can also apply the move to root heuristic to the search process as well, as we did for linked lists.
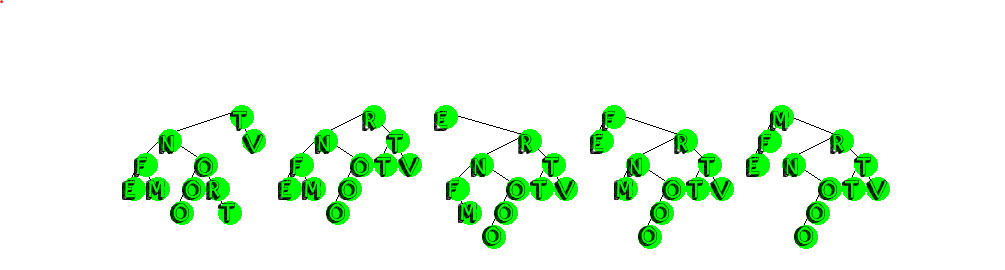
Node get(Node h, T info) {
if (h == nullptr || info == h->key)
return h;
if (info < h->key) {
h->left = get(h->left, info);
} else {
h->right = get(h->right, info);
}
return moveToRoot(h, info);
}
Compared to other types of binary search trees, deletion from these tree’s is incredibly simple: we perform a search for the key we are looking for, which if present brings it to the root of the tree, if at the root it has both right and left children, we merge its two children, setting the result as root. Otherwise, if the root has only one child, we set that child to root and we are done.
int size(Node h) {
if (h == nullptr)
return 0;
return 1 + size(h->left) + size(h->right);
}
Node partition(Node h, int k) {
if (h == nullptr)
return h;
int t = (h->left == nullptr) ? 0:size(h->left);
if (t > k) {
h->left = partition(h->left, k);
h = rotateRight(h);
}
if (t < k) {
h->right = partition(h->right, k - t - 1);
h = rotateLeft(h);
}
return h;
}
Node merge(Node a, Node b) {
if (b == nullptr) return a;
b = partition(b, 0);
b->left = a;
return b;
}
void remove(T info) {
Node result = get(m_root, info);
if (result != nullptr)
m_root = result;
if (m_root && m_root->key == info) {
m_root = merge(m_root->left, m_root->right);
m_count--;
}
}
You can actually make this method more efficient by removing the call to size() by tracking a node sub tree size at each node – being careful to update it during rotations. I implemented it using the external function call instead as part of the “appeal” of splay tree’s is that they don’t require storage beyond that need for pointers, and for the element its self.
It’s also worth mentioning that this his delete method works for more than just splay tree’s: just change the search portion to find the node to be deleted instead of additionally raising it to the root, and you can use this for regular BST and AVL trees. I suppose it could be modified to work with red black tree’s, but you’d need to pay attention to the node colors with all those rotations.
Comparison to Splay Trees
The modification to the insertion and search process laid out above set the ground work for what has come to be known as splay trees. Splay trees, like the search tree shown above keep the last accessed element at the root of the tree however, they make use of a more complicated rotation logic – as well as using double rotations in order to perform all operations in amortized O(log N) time.
Splay tree’s result in similarly balanced tree to Half-splay trees but use fewer overall rotations to do it. In this regard the comparison is kind of like the difference between Red/Black tree’s and AVL tree’s: The end result is similar, one just does a lot less work to get there.
Additionally, while splay tree’s can be created recursively, they are much, much easier to implement with the use of parent pointers. This is because rotations in splay tree’s are often based not just on a nodes relation to its parent, but also to it’s grand parent: something that while not impossible, is a bit more complicated in a recursive implementation with no parent pointers, as you have to start thinking several levels down, backwards, while being careful of null pointers.

