Ah tries, the tree structure with a name that nobody can agree on how to pronounce. Oddly spelled name aside, Tries offer a convenient way to implement a collection of strings in a way which supports operations such as finding the longest common prefix of two of strings extremely efficiently. They find uses in applications such as spell checking, IP address routing, and many other areas.
Unfortunately, the same properties that allows efficient lookups, is also incredibly inefficient when it comes to memory usage: this is one bulky data structure. The reason for this is that despite us using the trie to store strings as keys, the internal representation of those strings in a trie has a node to represent each individual character in the string, as well as a collection of pointers to its children – one for every possible character of our input alphabet!
#define ALPHASIZE 256 //there's 256 representable characters in ASCII
struct TrieNode {
char letter;
bool endOfString;
TrieNode* next[ALPHASIZE];
};
That’s not to say this a trait shared by all tries. As far as forest’s go, the trie family is diverse. On the complete opposite end of the spectrum from the prefix trie, is the family of “Digital Search Tries”, which includes amongst others, ternary search tree’s, and PATRICIA tries. What they gain in space efficiency, they unfortunately lose in difficulty of implementation(disregarding TST’s).
struct PatNode {
unsigned int b; //Patricia Trie's store single bit's as keys.
PatNode* left; //in addition to being binary trees, which
PatNode* right; //makes them very space efficient tries
};
Thankfully, their usefulness was recognized and finding efficient ways to implement tries has been an area of active research in computer science for quite some time. In this post I will be covering my own implementation of a Compressed Trie. The data structure I describe results in trees with the same split-key compressed paths as the PATRICIA algorithm produces, while loosening the restriction on being a binary tree, and a different way of deciding on making those splits. In recognition of PATRICIA tries inspiration, I have decided to call them SARLA Tries – for “Split And Re-Label” – the two fundamental operations performed.
Compressed Tries
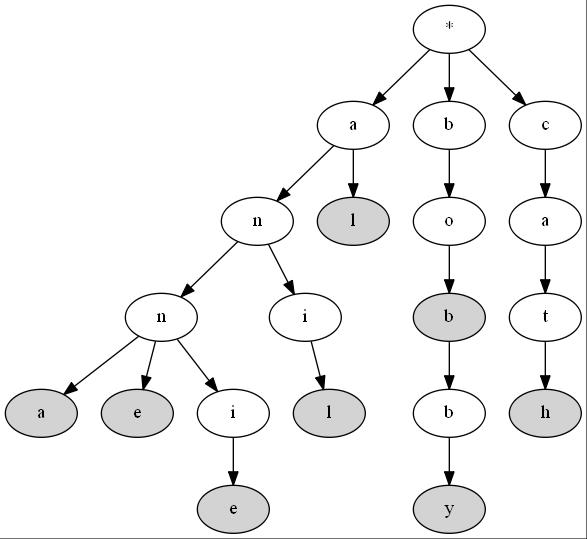
Looking at images of tries you may have noticed that a large majority of the nodes have a branching factor of one despite this low number of child nodes, man trie implementations allocate an array large enough to contain pointers for the entire input alphabet. The Trie pictured below has 26 child pointers, one for each uppercase letter, despite none of the node having more than two children! This is quite obviously very wasteful – especially considering each letter get its own node.
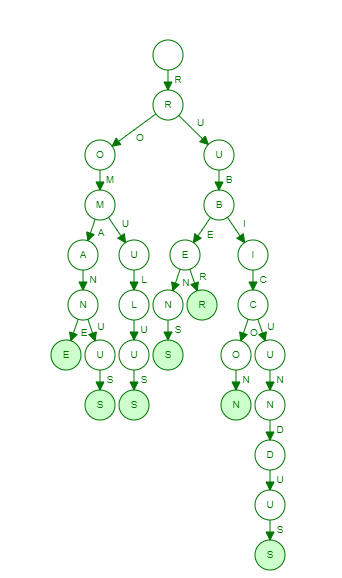
The reason for the one character per node implementation is that in a trie like the one pictured above, it’s not actually the node that is labeled. Tries have labeled edges and it is the concatenation of those edges by following them that we use to test for existence of a key in the trie. While this makes their implementation simple, it makes their memory usage extraordinary. Wouldn’t it be great if we could make the tree pictured above look something more like this? That’s exactly what SARLA Tries do.
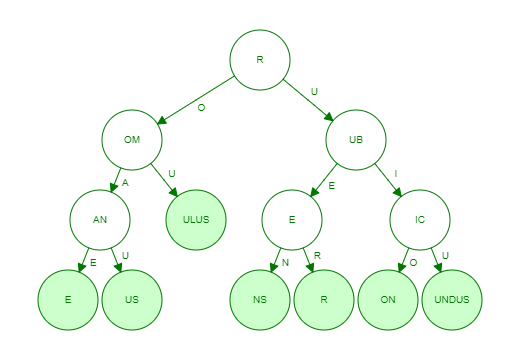
By converting edge labels to node labels, and combining characters that only have one child to form new substring keys we can drastically reduce the memory footprint of the trie while still maintaining efficient lookups.
Implementation
The first thing we need to do is change the Node representation for our Trie. Previously, we were concerned with only one letter at a time, but now we will be doing substring comparisons instead of character comparisons. To accommodate this change, the nodes will have strings for keys instead of chars.
struct CTNode {
string key;
map<char, CTNode*> next;
CTNode(string k = "") {
key = k;
}
};
As far as managing the child pointers go – i’m leaving that implementation detail up to you, though a few good choices are self balancing BST’s, hash tables, or any other efficient way of mapping a character key to a pointer you devise. For simplicities sake in this post, i’ll be using std::map. I believe that an LCRS rep binary tree would be a fantastic candidate for this particular trie, though i have only implemented insert and search for that particular implementation so can’t speak on its performance.
class CompressedTrie {
private:
using link = CTNode*;
link head;
int wordCount;
link insert(link node, string key);
bool contains(link node, string key);
public:
CompressedTrie();
void insert(string word);
bool contains(string word);
void levelorder();
};
There is a header node that’s only purpose is to route the algorithm to the correct subtree based on the first character of the key. Once on the proper subtree, path compression takes place top-down during the insertion phase. If we arrive at a null link we create a new node that will contain the remainder of the key that has not yet been consumed. At each node we compare our key to the current nodes key, unlike in uncompressed tries we have to check the keys for partial matches.
CTNode* insert(CTNode* root, string word) {
if (root == nullptr) {
return new CTNode(word);
}
int i = 0, j = 0;
link x = root;
while (i < word.length() && j < x->key.length())
if (word[i] == x->key[j]) {
i++; j++;
} else break;
string newWord = word.substr(i);
if (j == x->key.size()) {
x->next[newWord[0]] = insert(x->next[newWord[0]], newWord);
} else {
x = split(x, word, newWord, i, j);
}
return x;
}
There’s two special cases for insertion we need to address. First, if while comparing the keys we consume the entire nodes key, but not the word being inserted we continue by:
1) Extract the substring comprising the non-consumed letters of the input word.
2) insert the extracted subtring in the current node by calling insert recursively on the current node, with the sub string as the key.
For example, if we were inserting the word “newspaper” into a trie and the ‘n’ node is already occupied by the word “news”, we would continue by then inserting the substring “paper” into ‘p’ link of the current node(‘news’). Likewise, for the word ‘newsday’, we would continue by inserting ‘day’ into the ‘d’ position of the ‘news’ node.
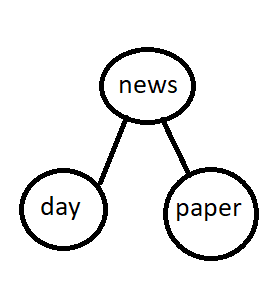
The second special case is If the keys diverge. This case is handled by the split method, which performs the the extracting of substrings and re-distribution of child nodes. If when comparing our insertion key to the current node, the keys diverge:
1) we create a new node using the characters that did match as it’s key, and insert it in the current nodes parent, (Split)
2) the substring created from the leftover characters in the current node’s key will become the current nodes new key (Re-Label).
This preserves any splits which occurred after the new key being inserted diverged. In this case, the tree actually grows upwards similar to a B-tree, instead of downwards when adding non-splitting keys.
CTNode* split(CTNode* x, string word, string newWord, int i, int j) {
string newkey = x->key.substr(0, j);
string rest = x->key.substr(i);
CTNode* t = new CTNode(newkey);
x->key = rest;
t->next[rest[0]] = x;
if (newWord.size() > 0)
t->next[newWord[0]] = insert(t->next[newWord[0]], newWord);
return t;
}
Keeping with our example from before, if we now insert the word “never” into our collection of words, the split() method gets called, resulting in the following trie:
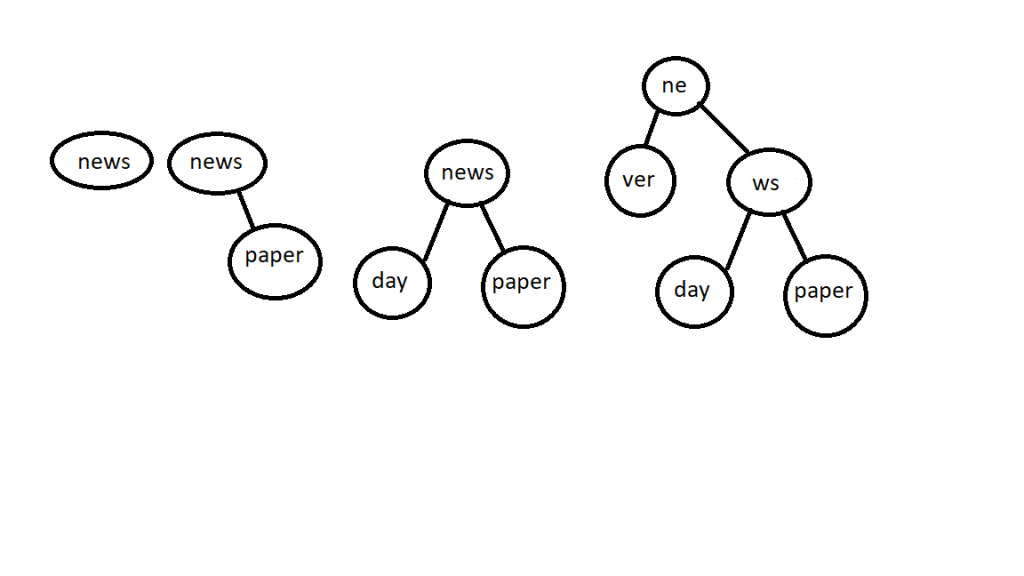
An additional bonus of using the split/relabeling algorithm is that it doesn’t overwrite keys that are prefixes of longer keys that get inserted. Instead, they are preserved by splitting the key being inserted to create a node from the words non-matching suffix.
Now that we can insert strings into our trie, we must also be able to retrieve them. This process is very similar to how it is performed in in a normal trie, We perform char-by-char comparisons of the keys, the difference being we have to chase far, far, fewer pointers in the process which makes this much faster than one your typical one-char-per-node implementations.
bool contains(string str) {
CTNode* x = head->next[str[0]];
int j = 0;
while (x != nullptr) {
int i = 0;
while (i < x->key.size() && j < str.size()) {
if (str[j] != x->key[i])
return false;
i++; j++;
}
if (j == str.size())
return true;
if (x->next.find(str[j]) == x->next.end())
return false;
else {
x = x->next[str[j]];
}
}
}
To traverse the tree, you build the strings incrementally, outputting the full string upon reaching a leaf node. An in-order traversal will yield the keys in lexicographically sorted order:
void traverse() {
for (auto p : head->next) {
string str = "";
preorder(p.second, str);
}
}
void traverse(nodeptr h, string& sofar) {
if (h == nullptr) return;
string curr = sofar + h->key;
if (h->next.empty()) {
cout<<curr<<endl;
} else {
for (auto child : h->next) {
traverse(child.second, curr);
}
}
}
If at first glance you thought that was a preorder traversal I wont fault you for it, but take my word for it, it’s an in-order traversal.
Counter to just about every other tree based data structure, erasing a key is fairly straight forward. The only nodes we ever have to remove from the tree is leaf nodes, as every node on the path above the leaf being removed is shared by a another entry.
The one tricky detail about removing keys from a trie – and this is true for any indexing data structure – erasing keys will leave artifacts behind: keys higher on the path whos descendants have been removed and who’s keys no longer match any previously inserted records. This is a side-effect of path compression being a one way algorithm.
nodeptr erase(nodeptr node, string key, string subkey) {
if (node == nullptr)
return node;
dbg.onEnter("Enter node " + node->key + " with key + " + key);
if (node->key == key && node->next.empty()) {
return nullptr;
}
int i = node->key.length();
string remainder = key.substr(i);
node->next[key[i]] = erase(node->next[key[i]], remainder, node->key.substr(0, i));
dbg.onExit("Exiting: " + node->key);
return node;
}
So there you have it: Compressed Tries without the fuss. That’s all I’ve got for today, Until next time happy Hacking!.
Further Reading
The wikipedia site on Radix Tree’s is where I got the list of ‘r’ words used in this post. It also has a good description of compressed tries, all be it in their binary form. https://en.wikipedia.org/wiki/Radix_tree
“Algorithms in C++” (3rd. ed) by Robert Sedgewick has a very thorough chapter on Radix searching that outlines various Trie based structures.
A full implementation is available on my github
